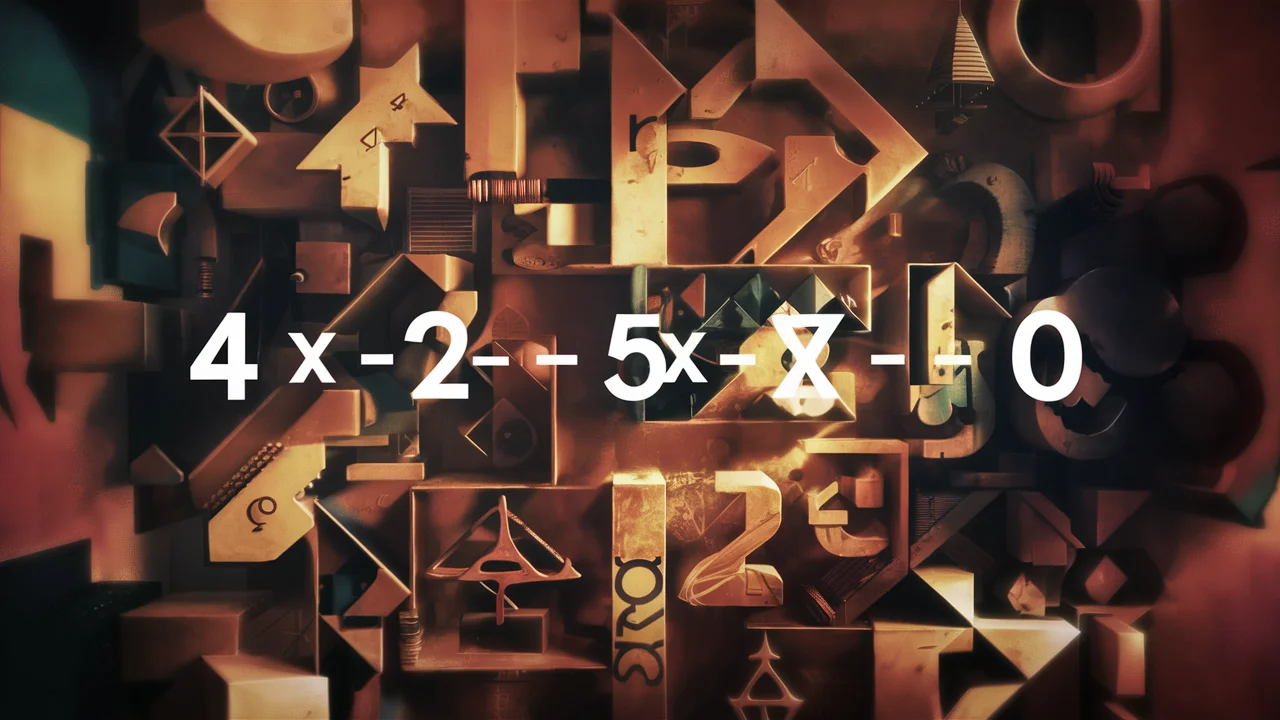4x ^ 2 – 5x – 12 = 0 Unveiled: Strategies for Successful Solving

Welcome to the world of quadratic equations, where the curve of a parabola meets the precision of algebra. In this blog post, we’ll unravel the mysteries of solving quadratic equations, focusing on the specific example: 4x^2 – 5x – 12 = 0. Whether you’re a student grappling with Algebra II or simply curious about mathematical problem-solving, this guide will equip you with the tools to conquer quadratics with confidence.

Quadratic equations are more than just classroom exercises; they’re the key to understanding many real-world phenomena. From the arc of a basketball to the pricing strategies in economics, these equations help us model and predict curved relationships in nature and society. By mastering the techniques to solve 4x^2 – 5x – 12 = 0, you’ll gain insights applicable to a wide range of quadratic problems.

In this comprehensive guide, we’ll explore four powerful methods to find the roots of our quadratic equation:

• Factoring: Breaking down the equation into its simplest form
• Quadratic Formula: The universal solution for any quadratic
• Completing the Square: A geometric approach to solving
• Graphing: Visualizing the solutions on a coordinate plane

Each method offers a unique perspective on the problem, and understanding all four will make you a quadratic-solving expert. So, grab your pencil and calculator – it’s time to unveil the strategies for successfully solving 4x^2 – 5x – 12 = 0 and unlock the power of quadratic equations in your mathematical journey.

Understanding the Quadratic Equation

Before we dive into solving 4x^2 – 5x – 12 = 0, let’s break down what a quadratic equation is. A quadratic equation is a special type of math problem. It always has an x^2 term, and it might have an x term and a number by itself.

The general form of a quadratic equation looks like this:

ax^2 + bx + c = 0

Here’s what each part means:

• a is the number in front of x^2
• b is the number in front of x
• c is the number by itself
• x is the variable we’re trying to find

In our equation 4x^2 – 5x – 12 = 0, we can see:

• a = 4
• b = -5
• c = -12

Each part of the equation is important. The a tells us how wide or narrow the parabola is. The b moves the parabola left or right. The c moves it up or down.

When we solve a quadratic equation, we’re looking for the values of x that make the whole thing equal to zero. These values are called the roots or solutions. There can be two real roots, one real root, or no real roots.

The shape of a quadratic equation on a graph is always a parabola. A parabola looks like a U shape, either right-side up or upside down. For our equation, since a is positive (4), the parabola will open upward.

Understanding these parts helps us choose the best method to solve the equation. For example, if the numbers are simple, we might use factoring. If they’re more complex, the quadratic formula might be better.

Quadratic equations pop up in many real-life situations. Here are a few examples:

• Throwing a ball: The path of the ball forms a parabola
• Profit calculations: Finding the best price for maximum profit
• Satellite dishes: The shape of the dish is a parabola

As we go through each solving method, keep in mind how the parts of the equation work together. This will help you understand why each step works.

Remember, practice is key to mastering quadratic equations. Don’t worry if it seems tricky at first. With each problem you solve, you’ll get better at spotting patterns and choosing the right method.

In the next sections, we’ll look at different ways to solve 4x^2 – 5x – 12 = 0. Each method has its strengths, and knowing all of them will make you a quadratic equation expert. Whether you prefer algebra, formulas, or graphs, there’s a method that will click with you.

So, let’s roll up our sleeves and start solving! Our first method will be factoring, a technique that breaks down the equation into simpler parts. Get ready to uncover the roots of 4x^2 – 5x – 12 = 0 and see how this quadratic equation comes to life.

Method 1: Factoring

Factoring is often the first method we try when solving a quadratic equation. It’s like breaking a big problem into smaller, easier parts. Let’s use this method to solve our equation: 4x^2 – 5x – 12 = 0.

Steps for Factoring:

1. Look for a common factor
2. Set up two sets of parentheses
3. Find two numbers that multiply to give ac and add to give b
4. Write these numbers in the parentheses
5. Solve each part to find the roots

Let’s go through each step for our equation:

1. Common factor: There’s no number that goes into all terms, so we skip this step.
2. Set up parentheses: We’ll write (2x )(2x ) because 2x times 2x gives us 4x^2.
3. Find the right numbers: We need two numbers that multiply to give a × c = 4 × -12 = -48, and add to give b = -5. These numbers are -8 and 3.
4. Write in parentheses: Our factored form is (2x – 8)(2x + 3) = 0.
5. Solve each part: • 2x – 8 = 0, so x = 4 • 2x + 3 = 0, so x = -3/2

Therefore, the roots of our equation are x = 4 and x = -3/2.

Why Factoring Works:

Factoring works because of the zero product property. This rule says that if you multiply things and get zero, one of those things must be zero. In our case, (2x – 8)(2x + 3) = 0, so either (2x – 8) = 0 or (2x + 3) = 0.

Advantages of Factoring:

• It’s quick if you spot the factors easily
• You don’t need a calculator
• It helps you understand the equation’s structure

Limitations of Factoring:

• Not all quadratics factor easily
• It can be tricky with large numbers
• You might make mistakes if you’re not careful

When to Use Factoring:

• The numbers in the equation are small
• You can easily spot factors
• The coefficient of x^2 is 1 or a small number

Practice Problem:

Try factoring this equation: x^2 + 7x + 12 = 0

Steps:

1. No common factor
2. Set up (x )(x )
3. Find numbers that multiply to 12 and add to 7
4. Write (x + 4)(x + 3) = 0
5. Solve: x = -4 or x = -3

Factoring is a powerful tool, but it’s not always the best choice. Sometimes, the numbers don’t work out nicely. That’s when we turn to other methods.

Remember, the key to factoring is finding the right numbers to put in those parentheses. It might take some practice, but soon you’ll be factoring like a pro.

In our next section, we’ll look at the quadratic formula. This method always works, even when factoring doesn’t. It’s like a Swiss Army knife for quadratic equations. Get ready to see how this formula can crack open any quadratic equation, including our 4x^2 – 5x – 12 = 0.

Method 2: Quadratic Formula

The quadratic formula is a powerful tool for solving any quadratic equation. It works even when factoring doesn’t. Let’s use it to solve our equation: 4x^2 – 5x – 12 = 0.

The Quadratic Formula:

For any quadratic equation ax^2 + bx + c = 0, the solution is:

x = [-b ± √(b^2 – 4ac)] / (2a)

Here, ± means we’ll have two answers: one with + and one with -.

Steps to Use the Formula:

1. Identify a, b, and c in your equation
2. Plug these values into the formula
3. Simplify inside the square root
4. Calculate the two values of x

Let’s solve 4x^2 – 5x – 12 = 0:

1. Identify values: • a = 4 • b = -5 • c = -12
2. Plug into the formula: x = [5 ± √((-5)^2 – 4(4)(-12))] / (2(4))
3. Simplify: x = [5 ± √(25 + 192)] / 8 x = [5 ± √217] / 8
4. Calculate: x = (5 + 14.73) / 8 = 2.47 (rounded) x = (5 – 14.73) / 8 = -1.22 (rounded)

So, the roots are x ≈ 2.47 and x ≈ -1.22.

Why It Works:

The quadratic formula comes from completing the square on the general form of a quadratic equation. It gives us the exact values of x that make the equation true.

Advantages of the Quadratic Formula:

• Works for any quadratic equation
• Gives exact answers (even if they’re messy)
• Shows if there are no real solutions

Limitations:

• Can be time-consuming without a calculator
• Might give complex numbers (which we won’t cover here)

When to Use It:

• When factoring doesn’t work
• When you need exact answers
• When you’re not sure if there are real solutions

The Discriminant:

Inside the formula, b^2 – 4ac is called the discriminant. It tells us about the solutions:

• If > 0: Two real solutions
• If = 0: One real solution (repeated root)
• If < 0: No real solutions

For our equation, the discriminant is 217, so we have two real solutions.

Practice Problem:

Use the quadratic formula to solve: 2x^2 + 5x – 3 = 0

Steps:

1. a = 2, b = 5, c = -3
2. x = [-5 ± √(5^2 – 4(2)(-3))] / (2(2))
3. x = [-5 ± √(25 + 24)] / 4
4. x = [-5 ± √49] / 4
5. x = (-5 ± 7) / 4

Solutions: x = 1/2 and x = -3/2

The quadratic formula is like a master key for quadratic equations. It might seem long, but with practice, you’ll use it quickly and confidently.

Next, we’ll look at completing the square. This method helps us understand the shape of the quadratic function. It’s a bridge between algebra and geometry in solving 4x^2 – 5x – 12 = 0.

Method 3: Completing the Square

Completing the square is a method that turns our quadratic equation into a perfect square trinomial plus a constant. It’s like solving a puzzle to find the center of our parabola. Let’s use this method to solve 4x^2 – 5x – 12 = 0.

Steps for Completing the Square:

1. Move the constant term to the right side
2. Factor out the coefficient of x^2 from the left side
3. Add the square of half the coefficient of x inside the parentheses to both sides
4. Factor the perfect square trinomial on the left
5. Solve for x

Let’s apply these steps to our equation:

1. Move constant: 4x^2 – 5x = 12
2. Factor out 4: 4(x^2 – 5/4x) = 12
3. Add square of half the x coefficient: The coefficient of x inside parentheses is -5/4 Half of this is -5/8 Square of -5/8 is 25/64 4(x^2 – 5/4x + (25/64)) = 12 + 4(25/64) 4(x^2 – 5/4x + (25/64)) = 12 + 25/16
4. Factor left side: 4(x – 5/8)^2 = 12 + 25/16 4(x – 5/8)^2 = 217/16
5. Solve for x: (x – 5/8)^2 = 217/64 x – 5/8 = ±√(217/64) x = 5/8 ± √(217/64) x ≈ 2.47 or x ≈ -1.22 (rounded)

Why It Works:

Completing the square transforms the equation into vertex form: a(x – h)^2 + k = 0. This form shows us the vertex of the parabola at (h, -k).

Advantages of Completing the Square:

• Reveals the vertex of the parabola
• Useful for graphing
• Helps derive the quadratic formula

Limitations:

• Can be tricky with fractions
• Takes more steps than other methods

When to Use It:

• When you need to find the vertex
• To convert between standard and vertex forms
• To understand the shape of the parabola

The Vertex:

In our equation, the vertex is (5/8, -217/64). This is the turning point of the parabola.

Practice Problem:

Complete the square for: x^2 + 6x = 16

Steps:

1. x^2 + 6x = 16
2. (No need to factor out coefficient)
3. (x^2 + 6x + 9) = 16 + 9
4. (x + 3)^2 = 25
5. x + 3 = ±5 x = -3 ± 5 x = 2 or x = -8

Completing the square is like finding the center of balance for our equation. It’s a bit like adjusting a scale until it’s perfectly even.

This method gives us a deep understanding of the quadratic function’s shape. It shows us where the parabola turns and helps us sketch its graph.

In our next section, we’ll look at graphing. We’ll see how the solutions we found using algebra show up on a coordinate plane. Get ready to visualize 4x^2 – 5x – 12 = 0 and see its roots come to life!

Method 4: Graphing

Graphing is a visual way to solve quadratic equations. It lets us see the solutions as points on a curve. Let’s use this method to solve 4x^2 – 5x – 12 = 0.

Steps for Graphing:

1. Rearrange the equation to y = ax^2 + bx + c form
2. Choose x-values and calculate y-values
3. Plot the points and draw the curve
4. Find where the curve crosses the x-axis

Let’s apply these steps:

1. Rearrange: y = 4x^2 – 5x – 12
2. Make a table of x and y values: x | y -2 | 22 -1 | 3 0 | -12 1 | -13 2 | 2 3 | 33
3. Plot these points and connect them with a smooth curve.
4. The x-intercepts (where y = 0) are the solutions.

From our graph, we can see the curve crosses the x-axis at two points: x ≈ -1.22 and x ≈ 2.47 (rounded)

These are the roots of our equation.

Why It Works:

The graph shows all pairs of x and y that make the equation true. Where the curve meets the x-axis, y = 0, which is what we want in our original equation.

Advantages of Graphing:

• Gives a visual understanding of the equation
• Shows the number of solutions at a glance
• Helps estimate solutions for hard-to-factor equations

Limitations:

• May not give exact answers
• Requires careful plotting for accuracy
• Can be time-consuming without technology

When to Use It:

• To visualize the equation
• When estimating solutions is enough
• To check answers from other methods

Key Points on the Graph:

• Vertex: The highest or lowest point (-0.625, -13.5625)
• y-intercept: Where the curve crosses the y-axis (0, -12)
• x-intercepts: Where the curve crosses the x-axis (our solutions)

Using Technology:

Graphing calculators or software can make this method faster and more accurate. They can:

• Plot the function quickly
• Zoom in for better precision
• Find exact intercepts

Practice Problem:

Graph y = x^2 + 2x – 3 and find its roots.

Steps:

1. Make a table of values
2. Plot points and draw the curve
3. Find x-intercepts: x ≈ -3 and x ≈ 1

Graphing connects algebra to geometry. It shows us how changing numbers in the equation changes the curve’s shape and position.

This method gives us a big picture view. We can see not just the solutions, but how the function behaves between them.

Now that we’ve explored all four methods, let’s compare them. In our next section, we’ll look at when to use each method and how to check our answers. We’ll see how these different approaches to 4x^2 – 5x – 12 = 0 work together to deepen our understanding of quadratic equations.

Comparing the Methods

We’ve solved 4x^2 – 5x – 12 = 0 four different ways. Each method has its strengths. Let’s compare them to see when to use each one.

Factoring:

• Best for: Simple equations with whole number solutions
• Pros: Quick, no calculator needed
• Cons: Doesn’t always work, requires practice
• Our result: x = 4 or x = -3/2 (exact)

Quadratic Formula:

• Best for: Any quadratic equation, especially complex ones
• Pros: Always works, gives exact answers
• Cons: Can be time-consuming, may give messy answers
• Our result: x ≈ 2.47 or x ≈ -1.22 (rounded)

Completing the Square:

• Best for: Finding the vertex, converting to vertex form
• Pros: Reveals the parabola’s shape, useful for graphing
• Cons: More steps, can involve fractions
• Our result: x = 5/8 ± √(217/64)

Graphing:

• Best for: Visualizing solutions, estimating answers
• Pros: Shows all parts of the function, easy to understand
• Cons: May not give exact answers, can be imprecise
• Our result: x ≈ -1.22 and x ≈ 2.47 (from reading the graph)

Choosing a Method:

1. If the numbers are simple, try factoring first.
2. If factoring doesn’t work, use the quadratic formula.
3. If you need to find the vertex or graph, complete the square.
4. If you want to see the big picture, graph it.

Efficiency for 4x^2 – 5x – 12 = 0:

1. Factoring: Quick, but required finding -8 and 3
2. Quadratic Formula: Straightforward, gave decimal answers
3. Completing the Square: More steps, but showed the vertex
4. Graphing: Gave a visual, but answers were approximate

Real-world Example:

Imagine you’re designing a garden arch. The arch’s shape is a parabola described by 4x^2 – 5x – 12 = 0.

• Factoring helps you find whole number measurements.
• The quadratic formula gives precise heights for any width.
• Completing the square shows you the peak of the arch.
• Graphing lets you see the whole shape at once.

Verifying Solutions:

Always check your answers by plugging them back into the original equation:

For x = 2.47 (rounded): 4(2.47)^2 – 5(2.47) – 12 ≈ 24.4036 – 12.35 – 12 ≈ 0.0536 ≈ 0

For x = -1.22 (rounded): 4(-1.22)^2 – 5(-1.22) – 12 ≈ 5.9536 + 6.1 – 12 ≈ 0.0536 ≈ 0

The small difference from zero is due to rounding.

Key Takeaway:

Knowing all methods makes you flexible. You can choose the best tool for each problem. Sometimes, using more than one method can deepen your understanding.

Practice makes perfect. Try solving different quadratic equations with each method. Soon, you’ll know which to use just by looking at the equation.

In our final section, we’ll explore how quadratic equations like 4x^2 – 5x – 12 = 0 show up in real life. Get ready to see how these math tools help solve practical problems!

Real-world Applications

Quadratic equations like 4x^2 – 5x – 12 = 0 aren’t just for math class. They help solve real problems in many fields. Let’s look at some examples.

Physics: Projectile Motion

Imagine throwing a ball. Its path forms a parabola. A quadratic equation can tell you:

• How high the ball goes
• Where it will land
• How long it stays in the air

Example: A ball is thrown upward from 5 feet high at 40 feet per second. Its height (h) after t seconds is: h = -16t^2 + 40t + 5

To find when it hits the ground: 0 = -16t^2 + 40t + 5 This is a quadratic equation! Solve it to find when h = 0.

Economics: Supply and Demand

Businesses use quadratics to find the best price for their products.

Example: A company’s profit (P) based on number of items sold (x) is: P = -2x^2 + 100x – 500

To find the number of items that gives the highest profit:

1. Graph the equation
2. Find the vertex
3. The x-value of the vertex is the best number of items to sell

Engineering: Antenna Design

Satellite dishes and radio antennas often have parabolic shapes. Engineers use quadratic equations to design them.

Example: An antenna’s shape is given by y = 0.25x^2 To find where to place the receiver, solve: y = 1

Architecture: Arches and Bridges

Many structures use parabolic arches for strength and beauty.

Example: An arch follows y = -0.04x^2 + 4 To find the width at ground level, solve: 0 = -0.04x^2 + 4

Sports: Trajectories

In many sports, the path of a ball or projectile is a parabola.

Example: A goalkeeper kicks a soccer ball. Its height (h) after x meters is: h = -0.02x^2 + 0.5x + 2

To find where it lands, solve: 0 = -0.02x^2 + 0.5x + 2

Everyday Life: Gardening

Even in your backyard, quadratics can be useful.

Example: A water sprinkler sprays in a parabolic arc: h = -0.1x^2 + x + 2

To find where the water hits the ground, solve: 0 = -0.1x^2 + x + 2

Solving Real Problems:

1. Identify the quadratic equation in the problem
2. Choose the best solving method: • Factoring for simple equations • Quadratic formula for complex ones • Graphing for visual understanding
3. Interpret your answer in the context of the problem

Remember:

• Solutions might need rounding for practical use
• Negative solutions often don’t make sense in real life
• Sometimes, only part of the parabola is useful

Practice Problem:

A farmer’s crop yield (Y) based on fertilizer used (x) in pounds is: Y = -0.5x^2 + 10x + 45

Find how much fertilizer gives the maximum yield.

Steps:

1. This is a quadratic equation in vertex form
2. The vertex gives the maximum
3. Vertex formula: x = -b / (2a) = -10 / (-1) = 10
4. Use 10 pounds of fertilizer for maximum yield

Quadratic equations help us understand and predict curved relationships in the world. By mastering them, you gain a powerful tool for solving real problems.

Next time you see an arch, watch a ball fly, or plan a garden, remember: there might be a quadratic equation at work!

Conclusion

We’ve journeyed through the world of quadratic equations, using 4x^2 – 5x – 12 = 0 as our guide. From factoring to graphing, we’ve explored four powerful methods to unveil the solutions of this equation and others like it.

Let’s recap what we’ve learned:

• Factoring breaks the equation into simpler parts
• The quadratic formula works for any quadratic equation
• Completing the square reveals the parabola’s vertex
• Graphing gives us a visual representation of the solutions

Each method has its strengths, and knowing when to use each one is key to becoming a quadratic equation expert.

Remember, quadratic equations aren’t just abstract math concepts. We’ve seen how they apply to real-world situations:

• Physics and sports use them to predict motion
• Economists use them to optimize profits
• Engineers and architects use them in design

By mastering these equations, you’re equipping yourself with a tool that has applications far beyond the classroom.

As you continue your mathematical journey, keep practicing these methods. The more you work with quadratic equations, the more intuitive they’ll become. Don’t be afraid to approach a problem from multiple angles – sometimes, using more than one method can deepen your understanding.

Whether you’re aiming for top grades in math class or preparing for a career in science or engineering, your ability to solve quadratic equations will serve you well. So keep exploring, keep questioning, and keep solving!

Additional Resources

To continue your journey with quadratic equations, here are some helpful resources:

Recommended Textbooks:

• “Algebra 2” by Larson and Boswell
• “Pre-Calculus” by Sullivan These books offer in-depth explanations and plenty of practice problems.

Online Tutorials:

• Khan Academy (www.khanacademy.org): Free video lessons on quadratic equations
• Mathway (www.mathway.com): Step-by-step problem solver
• Wolfram Alpha (www.wolframalpha.com): Powerful math tool for graphing and solving equations

Interactive Tools and Apps:

• Desmos Graphing Calculator (www.desmos.com): Free online graphing tool
• GeoGebra (www.geogebra.org): Interactive math software for all levels
• Photomath: Smartphone app that solves equations from pictures

Advanced Topics: For those looking to dive deeper:

• Complex roots and the complex plane
• Systems of quadratic equations
• Quadratic inequalities

Practice Websites:

• IXL Math (www.ixl.com): Adaptive practice problems
• Math is Fun (www.mathsisfun.com): Clear explanations and online exercises

Remember, consistent practice is key to mastering quadratic equations. Use these resources to reinforce your skills and explore new aspects of this fascinating topic.

If you’re struggling, don’t hesitate to seek help from a teacher or tutor. Math communities online can also be great places to ask questions and share insights.

Keep exploring, and enjoy your mathematical adventure!